Iterative learning control (ILC) is widely used to control repetitive processes because of its ability to realize high tracking performance in spite of imperfect model knowledge and repeating disturbances. The key idea of ILC is to update the control signal iteratively based on measured data from previous trials:

\(
\begin{equation} u_{j+1}(k) = Q(\mathrm{q})\left[{u_{j}(k) + L(\mathrm{q})e_{j}(k+1) }\right], \end{equation}
\)

where \(Q(\mathrm{q})\) and \(L(\mathrm{q})\) are the Q-filter and the learning function, respectively.

Generally, my ILC research aims to solve the following questions:

• How to obtain robustness against model uncertainty while still guarantee high tracking performance?
• Apply optimization tools to design ILC for optimal converged error and optimal convergence speed objectives
• Incorporate multiple ILC objectives in an ILC design: robustness, convergence speed, tracking performance and input constraint, and analyze trade-off between objective indices.

In norm-optimal ILC, the input signal for the next trial is generated by solving an optimization problem. This approach can deal with input constraints efficiently. The cost function relies on the system model, and hence model uncertainty can cause divergence and/or degrade performance of norm-optimal ILC. To deal with this problem, we propose a robust worst-case norm-optimal ILC design, where model uncertainty is taken into account:

\(
\begin{equation} \begin{array}{ll} \displaystyle\min_{u_{j+1}}\displaystyle\sup_{ \Delta \in \mathcal{B}_{\Delta}} J\left( {u}_{j + 1}, \Delta \right) \end{array} \end{equation}
\)

The design problem is reformulated as a convex optimization problem, and can be solved efficiently to obtain the optimal input signal for the next trial.

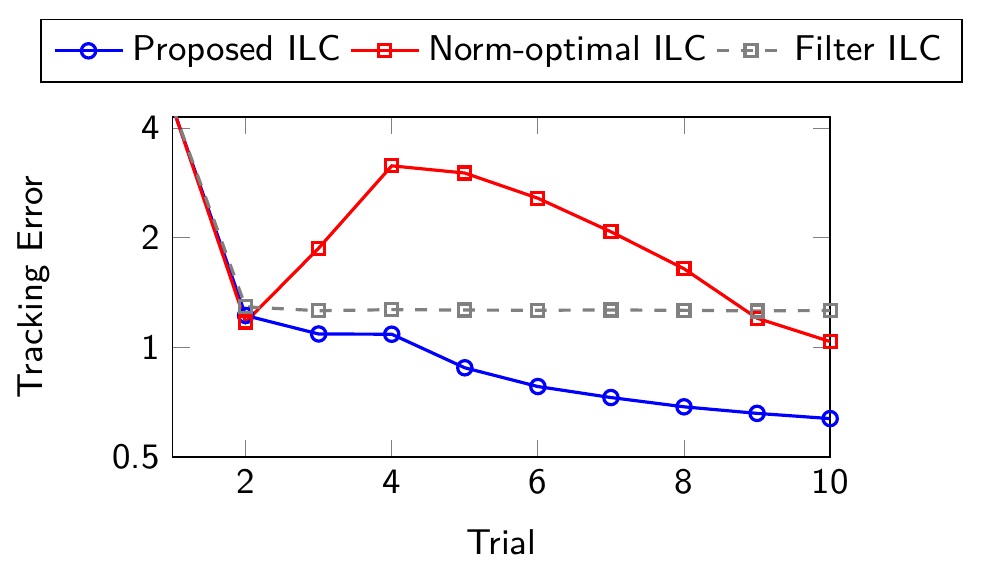
The robust controller is equivalent to an adaptive ILC design.

The proposed robust ILC design is experimentally validated on a lab scale overhead crane system, showing the advantages of the approach over classical ILC designs in monotonic convergence and tracking performance.

References:

Tong Duy, S., Pipeleers, G., Swevers, J., "Robust Monotonic Convergent Iterative Learning Control", IEEE Transaction on Automatic Control , Issue 99, July 2015

Tong Duy, S., Pipeleers, G., Swevers, J., "Experimental Validation of Robust Iterative Learning Control on an Overhead Crane Test Setup", The 19th World Congress of the International Federation of Automatic Control (IFAC14), Cape Town, Aug. 2014

The novelty of this work has two folds. First, we aim to design a one-step optimization based ILC design to solve for noncausal Q-filter and learning function simultaneously. Second, multiple ILC objectives are incorporated into our ILC algorithm:

\(
\begin{align} \begin{array}{ll} \displaystyle\min_{Q(\mathrm{q}),\; L(\mathrm{q})} & \text{convergence speed} \\ \text{subject to} & \text{robust convergence} \\ & \text{robust performance}\\ & \text{input constraint}. \end{array} \end{align}
\)

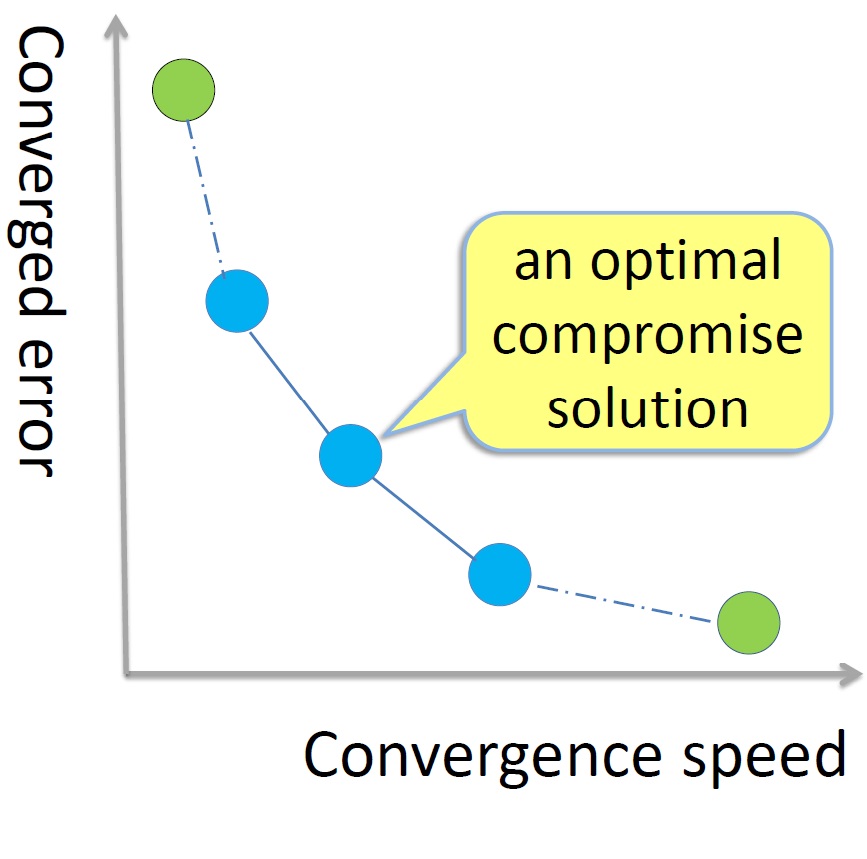
We reformulate the problem as a convex problem, guaranteeing an efficient and reliable computation of the global optimum and allowing straightforward computation of trade-off curves between different performance indices. These trade-off curves aid the control engineers in selecting their desired controller taking into account different objectives.

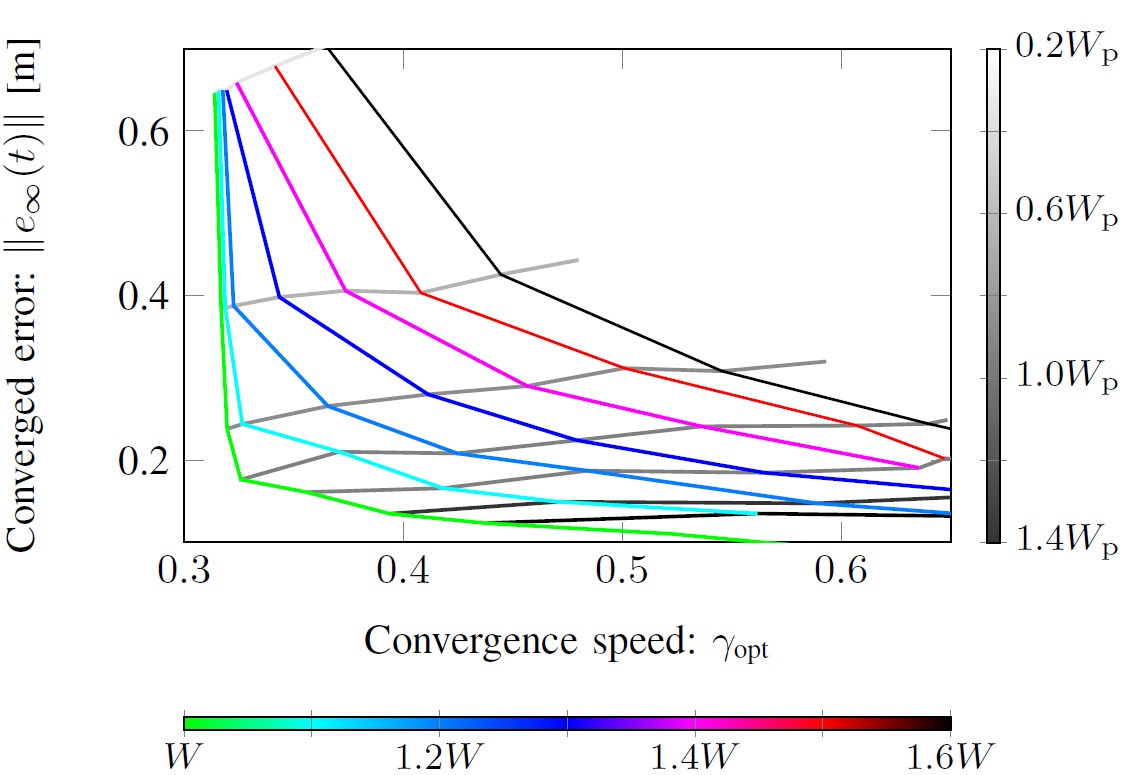
The figure show the trade-off curves with different converged error performance weighting function \(W_{\text{p}}(\mathrm{q})\) and uncertainty weighting function \(W(\mathrm{q})\) .

This work provides an effiient automated method for tuning ILC controller, and readily extended in many ways (i.e. model structure, ILC structure).

References:

Tong Duy, S., Pipeleers, G., Swevers, J., "Multi-objective Iterative Learning Control using Convex Optimization", European Journal of Control (submitted)

ILC system considers control task with finite time duration, leading to various ILC analyses and designs using the lifted system representation (i.e. learning matrices corresponds to the  number of samples in the system). In this research, my main contributions are:

• Proposed lifted system representation ILC robust convergence and robust performance analysis, taking into account model uncertainty
• Proposed ILC design for fastest convergence and smallest converged error objectives which are based on the proposed analyses

The results are validated numerically and experimentally on an XY-Table setup in the lab (collaboration with my colleague Armin Steinhauser).

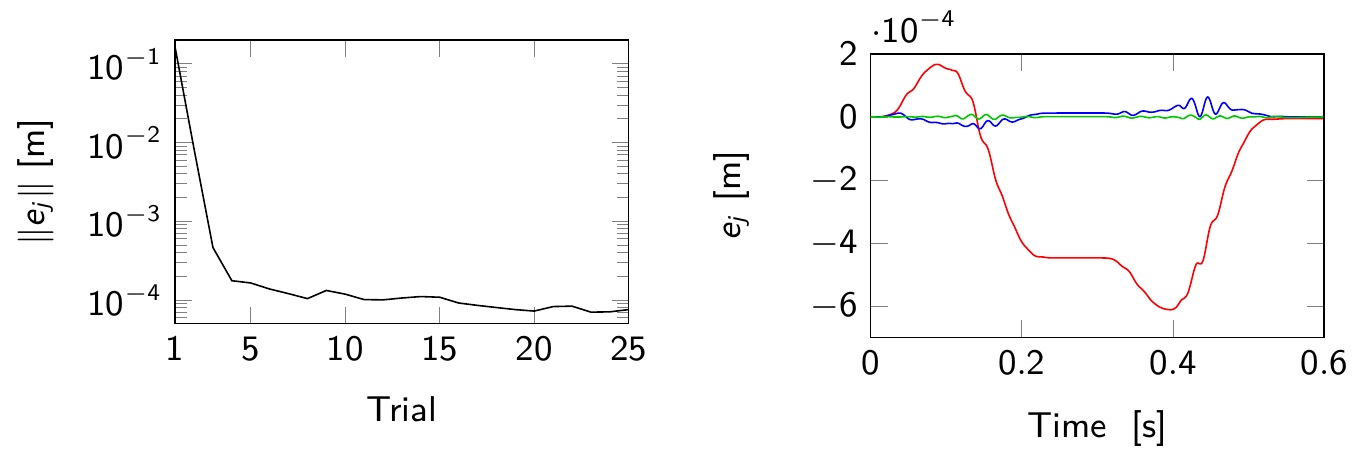
Tracking error norm in the trial domain (left) and tracking error in the time domain (trial 2(red), trial 3(blue), trial 25 (green)

References:

Tong Duy, S., Pipeleers, G., Swevers, J., "Robust Analysis and Synthesis with Unstructured Model Uncertainty in Lifted System ILC", 2015 American Control Conference (ACC15), , Chicago, IL, Jun. 2015

Tong Duy, S., Steinhauser, A., Pipeleers, G., Swevers, J., "Robust performance iterative learning control : Analysis, synthesis and experimental Validation", The European Control Conference (ECC16) (submitted) , Aalborg, Jul. 2016

This work is a part of my Marie Curie Initial Training Network: design feedback controller for the Amplifed Piezo Actuator (APA500L) of Cedrat Technologies (France) – a partner of the project. The task is to achieve high bandwidth tracking control for high-precision applications. I also spent my secondment in Cedrat Tech. for doing model identification.

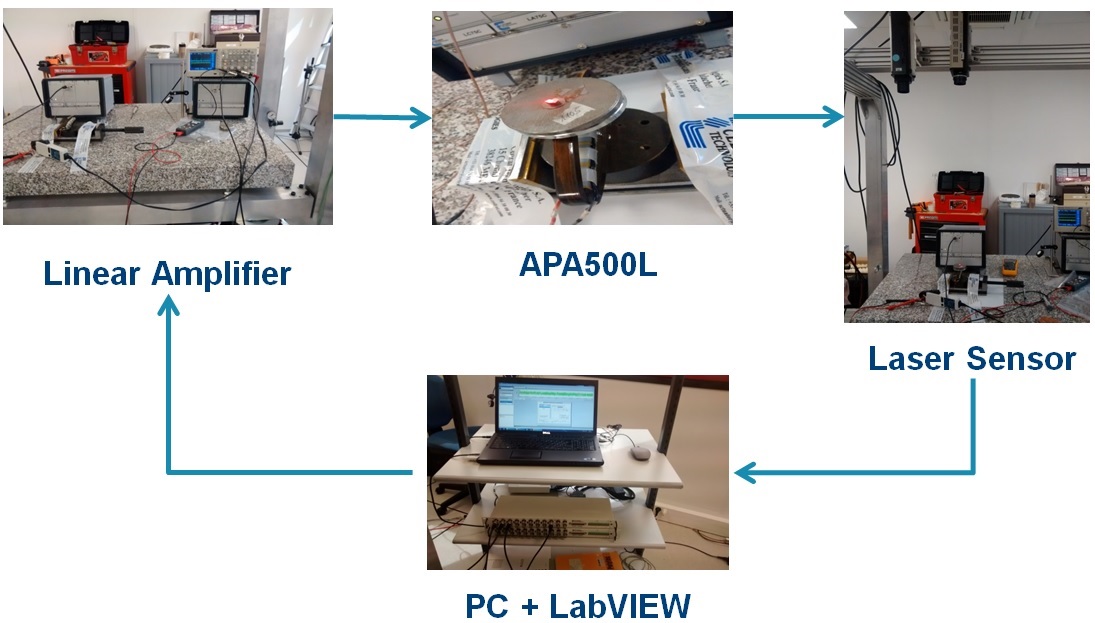
The figure shows the system setup diagram. The mixed-sensitivity loop shaping technique is considered for this application.

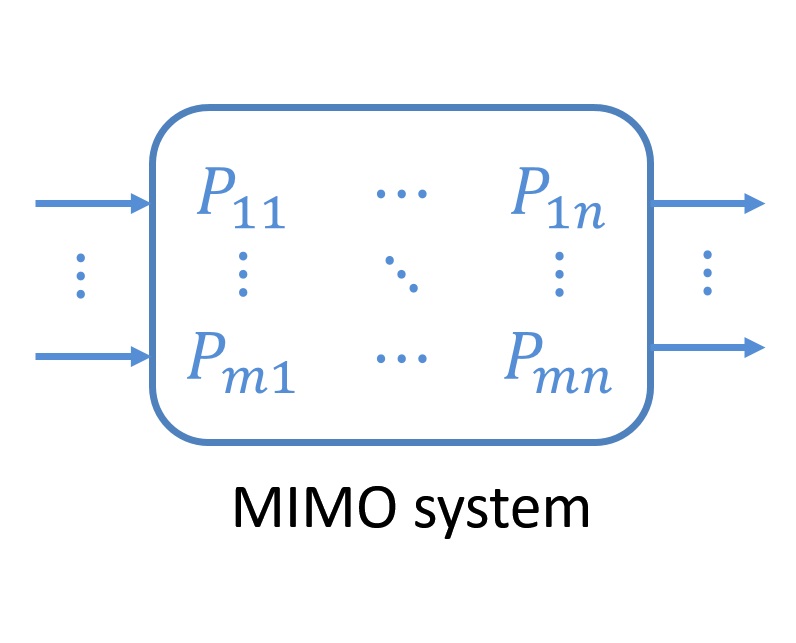
It is still a challenge to bring multivariable ILC to practical applications. The main reason is: most ILC algorithms in the literature rely on a two-step problem formulation (i.e. design learning function with the given Q-filter or vice versa) and the design procedures are usually heuristic. The parameter tuning steps are left to the designer. For example, a MIMO system of 5 inputs and 5 outputs will require tuning for 50 functions, which is almost impossible.

In this research, an automated tuning design for MIMO ILC is proposed to solve all non-causal learning gains simultaneously:

\(
\begin{align} \begin{array}{ll} \displaystyle\min_{Q(\mathrm{q}),\; L(\mathrm{q})} & {\bar\sigma} \big[{ Q (1 - L P) }\big], \; \forall \omega \;\;(1)\\ \text{subject to} & {\bar\sigma} \big[{ Q (1 - L P_\Delta) }\big] < 1, \; \forall\Delta \in \mathcal{B}_{\Delta},\; \forall \omega \;\;(2)\\ & {\bar\sigma}\big[{ W_{\mathrm{p}}\big({ I - P[I - Q(I - LP)]^{-1}QL}\big) }\big]\leq 1, \; \forall \omega \;\;(3)\\ & {\bar\sigma} \big[{ W_{\mathrm{u}} \big({ [I - Q(I - LP)]^{-1}QL }\big) }\big] \leq 1, \; \forall \omega \;\; (4). \end{array} \end{align}
\)

Here, (2) is the robust convergence condition, where both structured and unstructured uncertainty can be considered, (3) concerns tracking performance with the performance weight \(W_{\text{p}}(\mathrm{q})\) . (4) is the input constraint and the objective (1) corresponds to the convergence speed. The controller is considered of both linearly parameterized FIR and IIR filter types based on orthogonal basis functions:

\(
\begin{align} Q(\mathrm{q}) &= q_{0}\phi_{0}(\mathrm{q}) + q_{1}\phi_{1}(\mathrm{q}) + \ldots+ q_{n}\phi_{n}(\mathrm{q}) , \nonumber\\ \hat{L}(\mathrm{q}) &= \hat{l}_{0}\varphi_{0}(\mathrm{q}) +\hat{l}_{1}\varphi_{1}(\mathrm{q}) +\ldots+ \hat{l}_{m}\varphi_{m}(\mathrm{q}), \end{align}
\)

The proposed design is formulated as a convex problem of \(Q(\mathrm{q})\) and \(\hat{L}(\mathrm{q}) = {Q}(\mathrm{q}){L}(\mathrm{q})\) and the controller gains are guaranteed global solution and solved efficiently.

I am currently trying to furthur this research.